Questions:

[latexpage]
#MAASL00013

[Maximum Mark: 4]

Consider the infinite geometric sequence: $2, 2(0.8)^{1}, 2(0.8)^{2}, 2(0.8)^{3}$

a) Find $a_{10}$

b) Find the sum of this infinite geometric sequence

[latexpage]
#MAASL00041

[Maximum Mark: 5]

Consider the infinite geometric sequence $4, 4(0.6), 4(0.6)^{2}, 4(0.6)^{3},...$

a) Write down the $15th$ term of the sequence. Do not simplify the answer.

b) What is the sum of the infinite sequence?

[latexpage]
#MAASL00032

[Maximum Mark: 6] [Calc: Yes]


Examine these sequential diagrams

Diagram 1 consists 4 of line segments

a) Given that diagram $X$ consists of $901$ line segments, demonstrate that $X=300$ 

b) Solve for the sum of all line segments in the first $300$ diagrams

[latexpage]
#MAASL00004

[Maximum Mark: 6]

The first three terms of an arithmetic sequence are $u_{1}= 0.5, u_{2}= 1.8, u_{3}=3.1$

a) Find the common difference

b) Find the $30th$ term of the sequence

[latexpage]
#MAASL00158

[Maximum Marks: 6]

There is an infinite geometric series $6000, -3600, 2160, ...$

a) What is the ratio that exists?

b) What is the 5th term?

c) What is the exact sum?

[latexpage]
#MAASL00159

[Maximum Marks: 6]

There is an infinite geometric series $100, -50, 25, ...$

a) Determine the common ratio

b) What is the 7th term?

c) Determine the exact sum of the infinite geometric series.

[latexpage]
#MAASL00011

[Maximum Mark: 6]

In an Arithmetic Sequence, the first term is $2$ and the third term is $12$.

a) Find the common difference

b) Find the twentieth term

c) Find the sum of the first twenty terms of the sequence

[latexpage]
#MAASL00166

[Maximum Mark: 7]

a) Expand $\sum\limits_{r=4}^8 2^r$
 
b) $(i)$ Find the value of $\sum\limits_{r=4}^{25} 2^r$
 
$(ii)$ Explain why $\sum\limits_{r=4}^\infty 2^r$ cannot be evaluated 

[latexpage]
#MAASL00023

[Maximum Mark: 14]

Consider the geometric sequence in which the first term is $(20)$ and $r$= $\frac{1}{2}$

a) Find $u_{6}$

b) Find the sum of the infinite sequence

Consider the arithmetic sequences with the first term $(-18)$ and the eighth term $(-4)$

c) Find $d$

d) Show that $S_{n}= -19n+n^{2}$

e) Given that the sum of the infinite geometric sequence is equal to twice the sum of 
the arithmetic sequence, find $n$

[latexpage]
#MAASL00260

[Maximum Marks: 6]

There is an infinite geometric series $5000, -4200, 3528, ...$

a) What is the ratio?

b) What is the 6th term?

c) What is the exact sum of the series?

[latexpage]
#MAASL00261

[Maximum Mark: 6] [Calc: Yes]

               

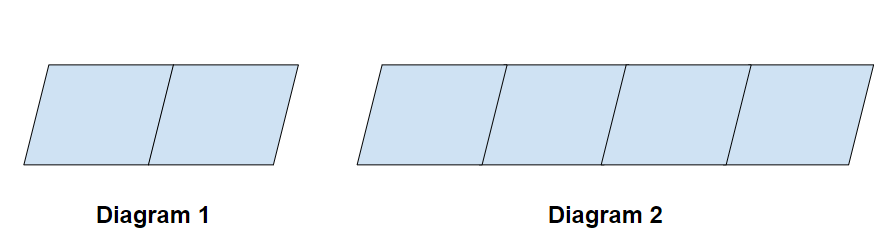Examine these sequential diagrams

Diagram 1 consists of 7 line segments

a) Given that diagram $X$ consists of $325$ line segments, demonstrate that $X=54$ 

b) Solve for the sum of all line segments in the first $23$ diagrams

[latexpage]
#MAASL00262

[Maximum Mark: 14]

Consider the geometric sequence in which the first term is $(24)$ and $r=\frac{1}{4}$

a) Find $u_{9}$

b) Find the sum of the infinite sequence

Consider the arithmetic sequences with the first term $(-12)$ and the sixth term $(-2)$

c) Find $d$

d) Show that $S_{n}= -13n+n^{2}$

e) Given that the sum of the infinite geometric sequence is equal to twice the sum of 
the arithmetic sequence, find $n$

[latexpage]
#MAASL00263

[Maximum Mark: 7]

a) Expand $\sum\limits_{r=2}^6 3^r$
 
b) $(i)$ Find the value of $\sum\limits_{r=2}^{22} 3^r$
 
$(ii)$ Explain why $\sum\limits_{r=2}^\infty 3^r$ cannot be evaluated 

[latexpage]
#MAASL00264

[Maximum Mark: 6]

Consider this following arithmetic sequence: 3, 11, 19, 27, 35...

a) Find the value of the 107th term.

b) Find $n$ so that $u_{n}=659$

[latexpage]
#MAASL00265

[Maximum Mark: 6]

Consider this following arithmetic sequence: 2, 6, 10, 14, 18...

a) Find the value of the 203rd term.

b) Find $n$ so that $u_{n}=3174$

[latexpage]
#MAASL00266

[Maximum Mark: 6]

Consider this following geometric sequence: 3, 9, 27, 81, 243...

a) Find the value of the 18th term.

b) Find $n$ so that $u_{n}=1594323$

[latexpage]
#MAASL00267

[Maximum Mark: 6]

Consider this following geometric sequence: 32, -16, 8, -4, 2...

a) Find the value of the 8th term.

b) Find $n$ so that $u_{n}=-\frac{1}{8}$

[latexpage]
#MAASL00268

[Maximum Mark: 6]

Consider the following arithmetic sequence: 97, 86, 75, 64, 53...

a) What is the common difference?

b) Find the 28th term of the sequence.

[latexpage]
#MAASL00269

[Maximum Mark: 6]

Consider the following geometric sequence: 87.75, 57.0375, 37.074375...

a) What is the common ratio?

b) Find the $S_{9}$.

[latexpage]
#MAASL00270

[Maximum Mark: 8]

Consider an arithmetic sequence with the following terms: $u_{1}=log_{a}(b)$ ; and $u_{2}=log_{a}(bc)$

In which: $a>1$ and $c>0$

a) Show that $d=log_{a}(c)$.

b) If $b=a^{3}$, and $c=a^{5}$, what is the value of $\sum\limits_{n=1}^{12} u_{n}$

In case you are looking for more help. This book includes 440 solved sequences and series questions. It is free for all Kindle users and generally pretty cheap to get anyways.